Formal language theory, language classes
In computer science, formal language is a field that studies formal languages.
Language definition
- A non-empty, finite set Σ is called an alphabet.
- An alphabet's elements are called letter, or character, or symbol.
- A (finite or infinite) subset of the power set of an alphabet is called a language.
Language classes

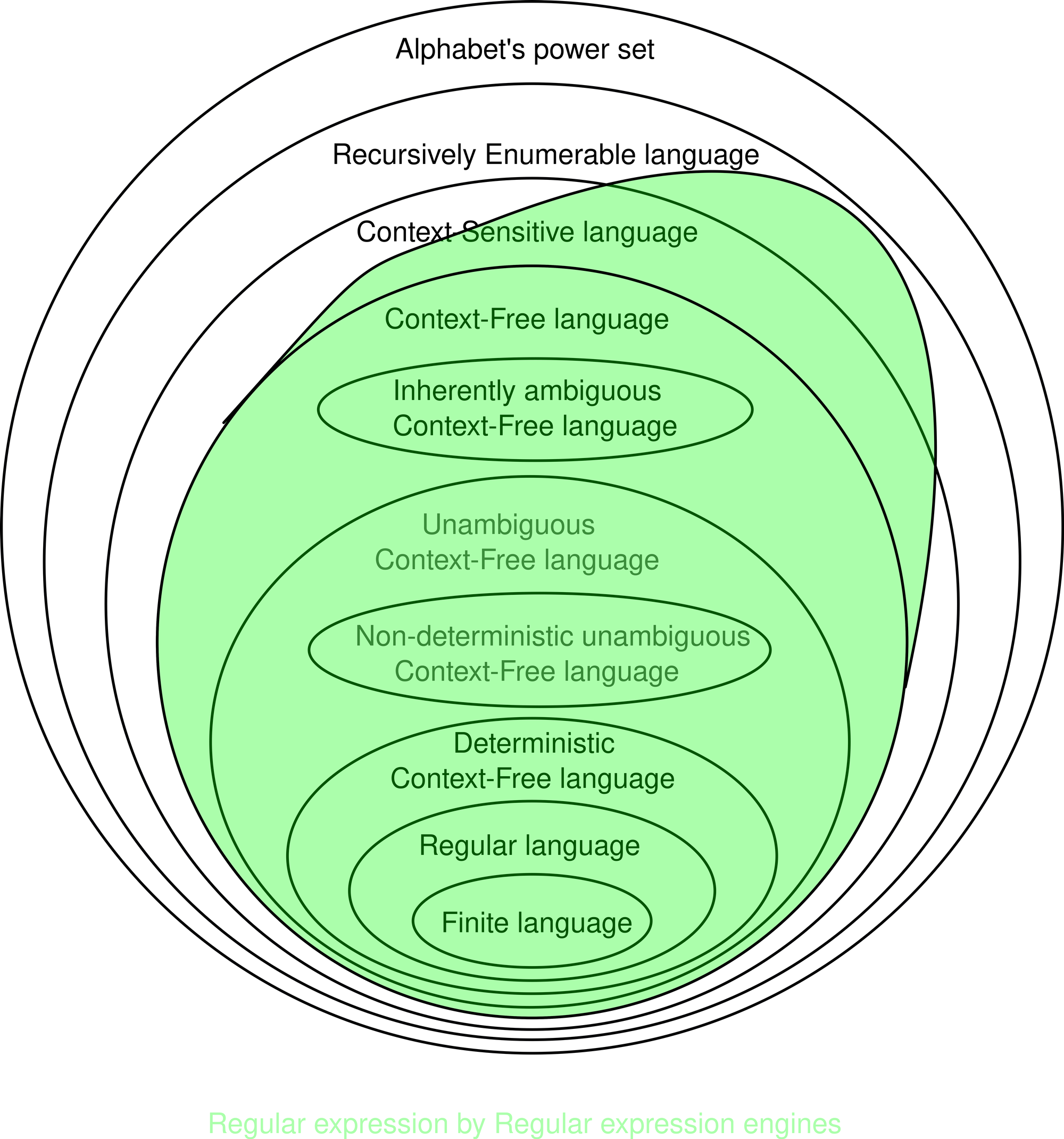
The above Venn diagram illustrates the relationship among language classes in formal language theory. Smaller and inside ovals present the associated language classes that are subsets of the languages associated with the container ovals.
Finite language
The finite language class consists of languages with a finite number of elements.
Example: {a, b, ab, c} is a finite language.
Regular language
There are several ways to define the regular language class. All these following definitions are equivalent.
- A regular language.
- A language is generated using a regular expression.
- A language is accepted by a Deterministic Finite Automaton.
- A language is generated by the regular grammar. A regular grammar is a grammar that is either left regular (left linear) or right regular (right linear).
Example: {an} is a regular language that isn't finite.
Caveats: Regular expression in formal theory, at the first hand, looks similar to the regular expression implemented by many regular expression engines (such as PCRE). However, they are totally different things.
Regular expression implemented by various regular expression engines is usually more powerful and is a superset of regular expression defined in formal theory.
Deterministic Context-Free language
Deterministic Context-Free language (DCFL) is a language accepted by a deterministic pushdown automaton.
Example: {anbncm} is a deterministic context-free language that isn't regular.
Note that DCFLs are always unambiguous and there exists an unambiguous context-free grammar that generates this language.
Unambiguous Context-Free language
A language that admits unambiguous context-free grammar.
Example: {wwR∣w∈{a,b}*}, {xnyn∣n≥0}∪{xny2n∣n≥0} are unambiguous and non-deterministic (source).
Inherently Ambiguous Context-Free language
A language whose generator context-free grammars are always ambiguous.
Example: {anbmcmdn|n>0,m>0}∪{anbncmdm∣n>0,m>0} is inherently ambiguous.
Context-Free language
Languages that admit context-free grammar, or equivalently, are accepted by a pushdown automaton.
Context-Sensitive language
Languages that admit context-sensitive grammar.
Example: {anbncn|n>0} (source).
Recursively enumerable language
A definition from Wikipedia.
A recursively enumerable language is a formal language for which there exists a Turing machine (or other computable function) that will halt and accept when presented with any string in the language as input but may either halt and reject or loop forever when presented with a string not in the language
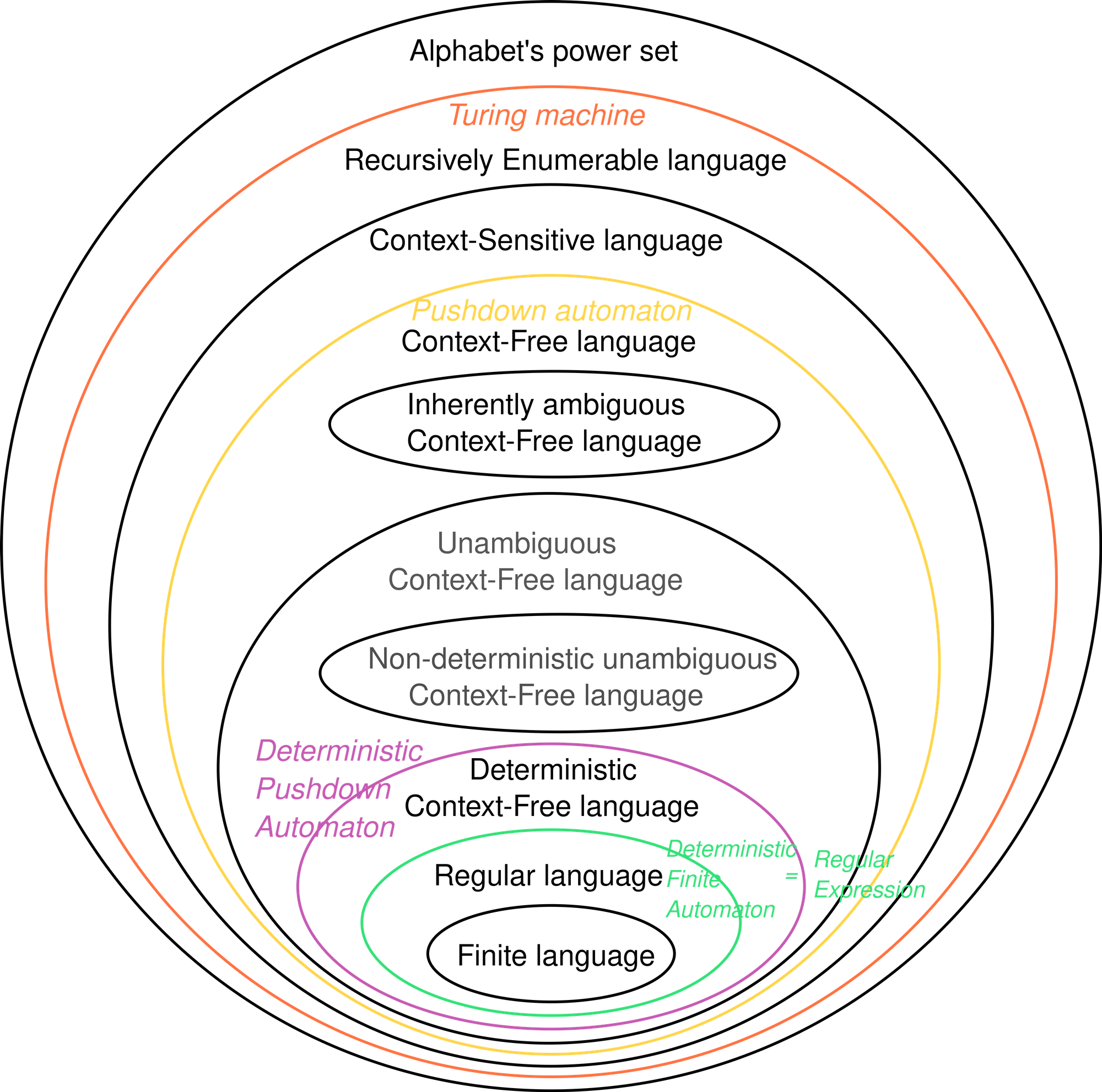
The following Venn diagram describes the relation between formal languages in formal theory and the theory of computation's automata.
Linear context-free grammar
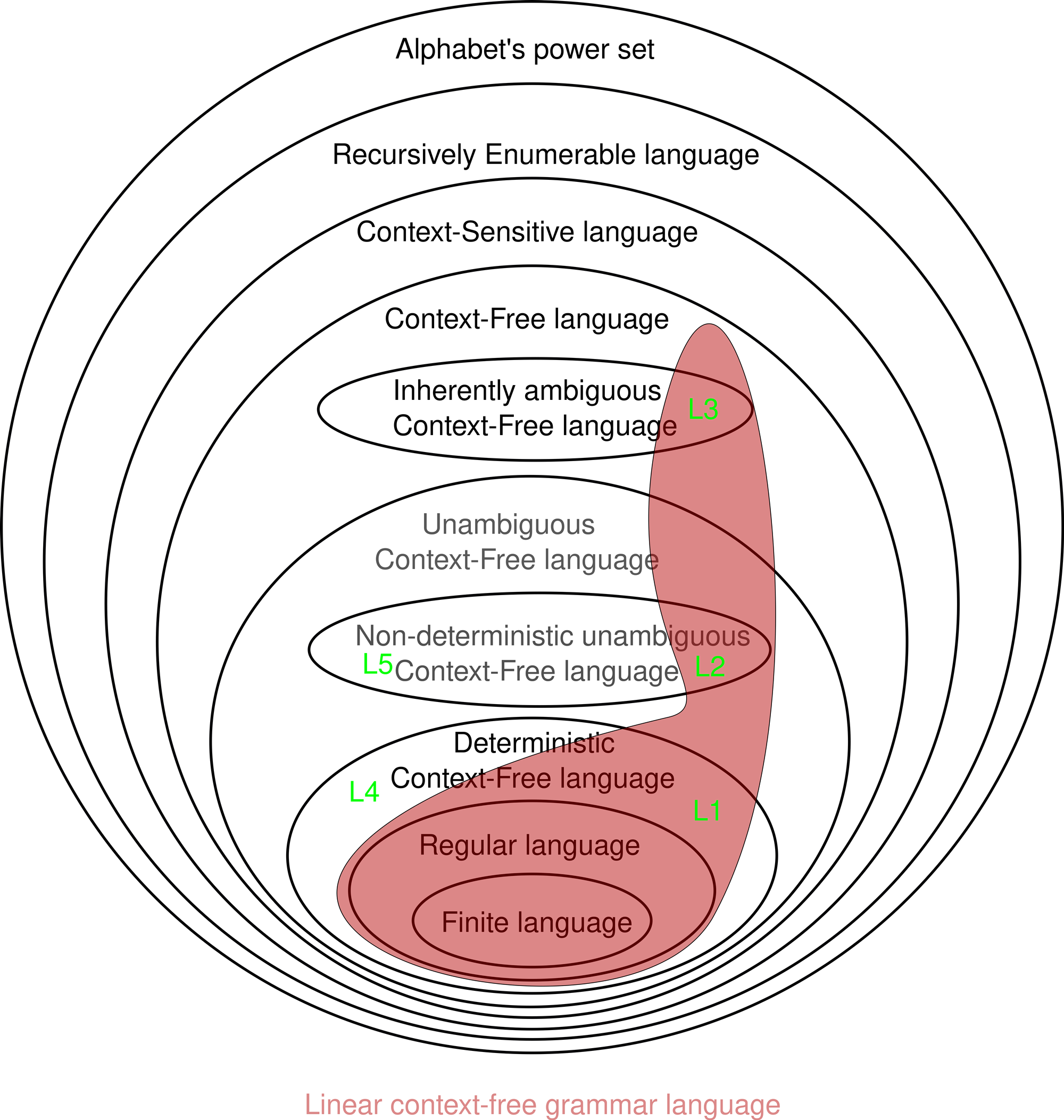
Note that: linear context-free grammar is not always left-linear or right-linear. For example: L1={anbn} is linear, deterministic, but non-regular (source).
Moreover, linear grammar can be nondeterministic. For instance: L2={wwR|w∈2Σ} is linear but nondeterministic (source).
Even stronger, a linear grammar language can be inherently ambiguous, such as L3={aibjck|i=j or j = k} (source).
A language L4 of well-formed brackets (such as (()(()))()) is non-linear but deterministic (and therefore, unambiguous).
Suppose L2 and L4 have different alphabets, L5=L2∪L4 is unambiguous, nonlinear, and non-deterministic.
Regular expression engine
As stated previously, regular express that is implemented by regular-expression engines in various languages, such as the well-known Perl Compatible Regular Expressions, is far different from the language class with the same name in formal language theory.
So, how strong is a regular expression engine?
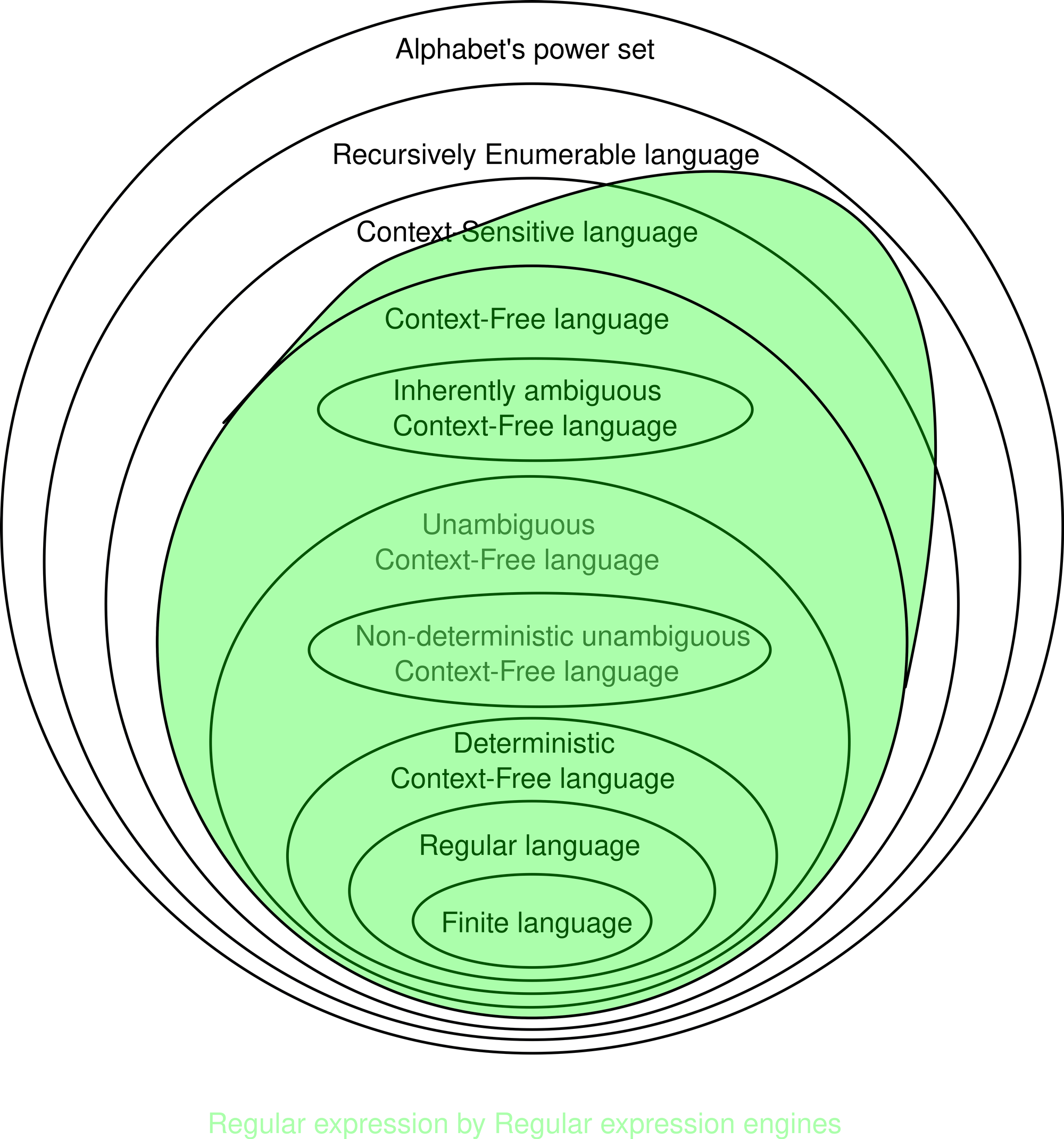
Take PCRE as an example, this engine can match any context-free language, some context-sensitive languages, and even is able to represent some unrestricted grammars. The reason for the more powerful capability of the regular expression engines compared to the regular expression in formal theory comes from several additional features such as backreference, conditioning, look around, etc...
There is proof provided here. (pdf snapshot).

